Einfache Moderationsanalyse (Model 1)

#01 Einleitung in Model 1

Eine regressionsbasierte Moderationsanalyse ist eine statistische Methode, die untersucht, wie die Beziehung zwischen einer unabhängigen Variablen (Prädiktor) und einer abhängigen Variablen (Kriterium) durch eine dritte Variable, den Moderator, beeinflusst wird. Im Kern geht es darum zu verstehen, wie und unter welchen Bedingungen bestimmte Effekte auftreten. Diese Analyseform ermöglicht es, die Bedingungen zu identifizieren, unter denen ein Prädiktor einen stärkeren oder schwächeren Einfluss auf das Ergebnis hat, indem sie die Interaktion zwischen dem Prädiktor und dem Moderator in das Modell einbezieht.

\(Y = b_{0} + b_{1}X_{1} + b_{2}X_{2} + b_{3}X_{1}X_{2} + E\)

Die Hinzunahme eines Moderators in eine Regressionsanalyse erweitert das grundlegende Regressionsmodell um einen Interaktionsterm, der das Produkt des Prädiktors (\( X_{1} \)) und des Moderators (\( X_{2} \)) darstellt. Dieser zusätzliche Term ermöglicht es, die Veränderungen in der Stärke und/oder Richtung der Beziehung zwischen dem Prädiktor und der abhängigen Variablen zu beurteilen, die durch den Moderator verursacht werden. Die Analyse liefert Einsichten darüber, ob die Wirkung des Prädiktors auf die abhängige Variable für verschiedene Werte oder Ebenen des Moderators variiert, wodurch differenziertere und kontextspezifischere Interpretationen der Daten möglich werden.

In der Praxis wird eine Moderationsanalyse in verschiedenen Forschungsfeldern angewandt, von der Psychologie über die Sozialwissenschaften bis hin zu den Wirtschaftswissenschaften, um komplexe Interaktionen zwischen Variablen zu verstehen und zu modellieren. Durch die Identifizierung von Moderatoren können Forschende gezieltere Hypothesen aufstellen und tiefere Einblicke in die Mechanismen gewinnen, die ihren Daten zugrunde liegen.

#02 process-Syntax

process kann entweder über die grafische Oberfläche unter:

„Analysieren“ -> „Regression“ -> „PROCESS v4.3 by Andrew F. Hayes“

oder über das Syntax-Fenster in SPSS Statistics genutzt werden. Die einfache Moderation wird als „Model 1“ bezeichnet. Ein beispielhafter Syntax-Befehl könnte wie folgt aussehen:

process y=AV/x=UV/w=MOD/model=1/center=1/plot=1/jn=1.

Für „AV“, „UV“ und „MOD“ müssen die eigenen Variablennamen eingesetzt werden. „process“ initialisiert das Makro und ist per Leerzeichen vom Rest des Syntax-Befehls getrennt. Mit model wird die gewünschte Modellvorlage bestimmt. center sorgt für das Zentrieren der Prädiktoren, die am Interaktionstermin beteiligt sind. Wenn „0“ ausgewählt wird, erfolgt keine Zentrierung; bei „1“ werden alle am Interaktionsterm beteiligten Prädiktoren zentriert; bei „2“ werden die metrischen Prädiktoren zentriert, die am Interaktionsterm beteiligt sind. plot erzeugt am Ende der Ergebnis-Ausgabe einen SPSS-Syntax-Schnipsel, der ein Liniendiagramm produziert, wenn „1“ gewählt wird. Die Standardeinstellung ist „0“ – also keine zusätzliche Syntax, wenn der Befehl nicht spezifiziert wird. Zuletzt wird mit jn die Johnson-Neyman-Technik genutzt, um Werte des Moderators zu identifzieren, bei denen der Effekt von X auf Y auf einem Niveau von 5% signifikant ist. Eine grundsätzliche Übersicht zur process-Syntax find Du auf unserer Seite process-Syntax.

#03 Beispiel

In einem plakativen Beispiel soll die einfache Moderationsanalyse in SPSS Statistics mithilfe von process durchgeführt werden. Betrachten wir in Anlehnung an Scheider & Schwark (2023), wie der Zusammenhang von Arbeitsleistung in Abhängigkeit der Home-Office-Intensität durch die organisationale Unterstützung moderiert wird. Auch wenn die beiden Autoren Hinweise auf kurvilineare Zusammenhänge zwischen Arbeitsleistung und Home-Office-Intensität gefunden haben, soll das nachfolgende Beispiel unter Annahme linearer Beziehungen betrachtet werden. Darüber hinaus sind die verwendeten Daten künstlich erzeugt.

Es gilt folgende Skalierung und Bezeichnung der Variablen:

AV = Arbeitsleistung (Skala 1 bis 7) – AL
UV = Home-Office-Intensität (Skala 1 bis 7) – HOI
Moderator = Organisationale Unterstützung (Skala 1 bis 7) – OU

Die Berechnungen finden auf Basis von 100 fiktiven Datensätzen statt – es werden keine Kovariaten festgelegt. Somit ergibt sich folgender Syntax-Befehl:

process y=AL/x=HOI/w=OU/model=1/center=1/plot=1/jn=1.

Es ist zu beachten, dass die process.sps Syntax-Datei einmalig nach dem Start von SPSS Statistics ausgeführt werden muss, damit das PROCESS-Makro funktioniert. Habe etwas Geduld, da das Ausführen dieser Datei einen Moment dauern kann.

#04 Ergebnis

Model Summary

R R-sq MSE F df1 df2 p

0.93 0.86 0.25 193.43 3 96 0.000

(Anmerkung: SPSS Statistics/process runden sehr kleine p-Wert auf 0.000. Das bedeutet natürlich auf keinen Fall, dass der p-Wert tatsächlich null ist, sondern eben sehr klein. In Anlehnung an die Empfehlungen der APA, wird ein solcher Wert mit „p < .001″ gekürzt.)

Der Model Summary-Abschnitt bietet einen Überblick über die Güte des Gesamtmodells. Das multiple R von 0.92 zeigt eine starke Korrelation zwischen den Prädiktoren und der abhängigen Variable. Das R-sq von 0.86 indiziert, dass etwa 86% der Varianz in der abhängigen Variable durch das Modell erklärt werden. Der mittlere quadratische Fehler (MSE) von 0.25 gibt Aufschluss über die durchschnittliche quadrierte Abweichung zwischen den vorhergesagten und den beobachteten Werten. Der F-Wert von 193.43 mit 3 (df1) und 96 (df2) Freiheitsgraden und einem p-Wert von 0.000 (p < .001) deutet auf eine statistische Signifikanz des Gesamtmodells hin.

Model Coefficients

Variable coeff se t p LLCI ULCI

constant 3.00 0.05 60.41 0.000 2.90 3.10

HOI 0.52 0.03 16.97 0.000 0.46 0.58

OU 0.42 0.03 14.15 0.000 0.36 0.48

Int_1 0.17 0.02 8.67 0.000 0.13 0.21

Der Model-Abschnitt präsentiert die Regressionskoeffizienten für jede Variable im Modell. Die Konstante (coeff = 3.00) repräsentiert den erwarteten Wert der abhängigen Variable, wenn alle Prädiktoren null sind. Der Koeffizient für HOI (coeff = 0.52) zeigt den direkten Effekt der Home-Office-Intensität auf die Arbeitsleistung. Der Koeffizient für OU (coeff = 0.42) repräsentiert den direkten Effekt der organisationalen Unterstützung. Der Interaktionsterm (Int_1) mit einem Koeffizienten von 0.17 (coeff) quantifiziert den Moderationseffekt. Alle Koeffizienten sind bei einem Signifikanzniveau von p = 0.000 (p < .001) statistisch signifikant, was durch die t-Werte und die Konfidenzintervalle (LLCI und ULCI) untermauert wird, die den Wert null nicht einschließen.

Test(s) of highest order unconditional interaction(s)

Interaction R2-chng F df1 df2 p

X*W 0.11 75.16 1 96 0.000

Dieser Abschnitt fokussiert sich auf die Signifikanz des Interaktionseffekts. Die Änderung in R-Quadrat (R2-chng) von 0.11 indiziert, dass die Hinzufügung des Interaktionsterms zusätzliche 11% der Varianz in der abhängigen Variable erklärt. Der F-Wert von 75.16 mit 1 (df1) und 96 (df2) Freiheitsgraden und einem p-Wert von 0.000 (p < .001) untermauert die statistische Signifikanz des Interaktionseffekts. Der p-Wert ist identisch mit dem p-Wert aus vorherige Tabelle des Moderationsterms (Int_1).

Conditional effects of the focal predictor at values of the moderator(s)

OU Effect se t p LLCI ULCI

-1.68 0.23 0.05 5.04 0.000 0.14 0.32

0.00 0.52 0.03 16.97 0.000 0.46 0.58

1.68 0.80 0.04 18.59 0.000 0.71 0.88

Dieser letzte Abschnitt illustriert den Effekt der Home-Office-Intensität (HOI) auf die Arbeitsleistung (AL) bei verschiedenen Ausprägungen der organisationalen Unterstützung (OU). Bei niedriger organisationaler Unterstützung (-1.68 Standardabweichungen unter dem Mittelwert) beträgt der Effekt 0.23. Bei durchschnittlicher organisationaler Unterstützung (0.00) steigt der Effekt auf 0.52, und bei hoher organisationaler Unterstützung (1.68 Standardabweichungen über dem Mittelwert) erhöht sich der Effekt weiter auf 0.78. Alle diese Effekte sind statistisch signifikant (p = 0.000 -> p < .001), was durch die Konfidenzintervalle gestützt wird, die den Wert null nicht einschließen. Dies demonstriert, dass der positive Effekt der Home-Office-Intensität auf die Arbeitsleistung mit zunehmender organisationaler Unterstützung verstärkt wird.

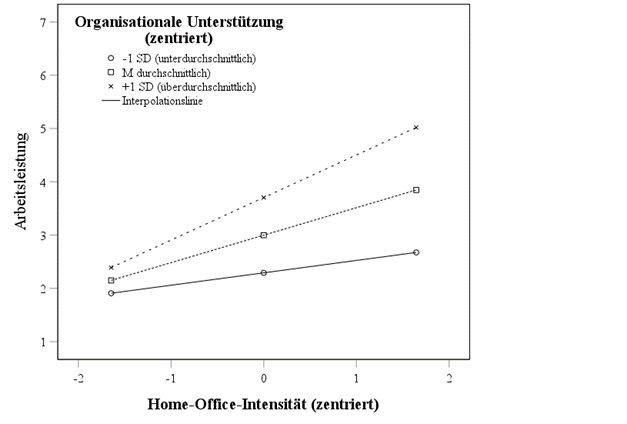
#05 Visualisierung

Neben der Analyse bedingter Haupteffekte bietet es sich an, die Ergebnisse einer Moderationanalyse zu visualisieren, wie mit der process-Syntax (/plot=1) angestoßen. Mit ein wenig nachträglicher Bearbeitung könnte das nachfolgende Diagramm dazu genutzt werden, um die Interpretation bzw. den nachfolgenden Ergebnisbericht zu erweitern.

Interaktionsdiagramm

Moderationsanalyse auf den Zusammenhang zwischen Arbeitsleistung und Home-Office-Intensität

#06 Interpretation

Eine Moderationsanalyse wurde durchgeführt, um den Einfluss der Home-Office-Intensität (HOI) auf die Arbeitsleistung (AL) unter Berücksichtigung des moderierenden Effekts der organisationalen Unterstützung (OU) zu untersuchen. Das Gesamtmodell erwies sich als statistisch signifikant (F(3, 96) = 193.43, p < .001) und erklärte einen großen Anteil der Varianz in der Arbeitsleistung (R² = .86).

Die Analyse ergab signifikante Haupteffekte sowohl für die Home-Office-Intensität (b = 0.52, SE = 0.03, p < .001, 95% KI [0.46, 0.58]) als auch für die organisationale Unterstützung (b = 0.42, SE = 0.03, p < .001, 95% KI [0.36, 0.48]). Darüber hinaus wurde ein signifikanter Interaktionseffekt zwischen HOI und OU festgestellt (b = 0.17, SE = 0.02, p < .001, 95% KI [0.13, 0.21]). Die Hinzufügung des Interaktionsterms zum Modell führte zu einer signifikanten Erhöhung der erklärten Varianz um 11% (F(1, 96) = 75.16, p < .001).

Um die Art der Interaktion genauer zu untersuchen, wurden bedingte Effekte der Home-Office-Intensität auf die Arbeitsleistung bei verschiedenen Ausprägungen der organisationalen Unterstützung berechnet. Bei niedriger organisationaler Unterstützung (1 SD unter dem Mittelwert) zeigte sich ein positiver Effekt der Home-Office-Intensität auf die Arbeitsleistung (b = 0.23, SE = 0.05, p < .001, 95% KI [0.14, 0.32]). Dieser Effekt verstärkte sich bei durchschnittlicher organisationaler Unterstützung (b = 0.52, SE = 0.03, p < .001, 95% KI [0.46, 0.58]) und war am stärksten bei hoher organisationaler Unterstützung (1 SD über dem Mittelwert; b = 0.80, SE = 0.04, p < .001, 95% KI [0.71, 0.88]).

Diese Ergebnisse deuten darauf hin, dass der positive Zusammenhang zwischen Home-Office-Intensität und Arbeitsleistung durch die organisationale Unterstützung moderiert wird. Spezifisch zeigt sich, dass mit zunehmender organisationaler Unterstützung der positive Effekt der Home-Office-Intensität auf die Arbeitsleistung verstärkt wird. Diese Befunde unterstreichen die Bedeutung organisationaler Unterstützung bei der Implementierung und Gestaltung von Home-Office-Arrangements, um deren positive Auswirkungen auf die Arbeitsleistung zu maximieren.

#07 Tabelle

	Arbeitsleistung
Variable	b (SE)	t	p	95% KI
Home-Office-Intensität^a	0.52 (0.03)	16.97	< .001	[0.46, 0.58]
Organisationale Unterstützung^a	0.42 (0.03)	14.15	< .001	[0.36, 0.48]
Home-Office-Intensität × Organisationale Unterstützung	0.17 (0.02)	8.67	< .001	[0.13, 0.21]
ΔR²	.11^b
R²	.86^c
Bedingte Haupteffekte
Organisationale Unterstützung	Home-Office-Intensität	t	p	95% KI
−1 SD	0.23 (0.05)	5.04	< .001	[0.14, 0.32]
M	0.52 (0.03)	16.97	< .001	[0.46, 0.58]
+1 SD	0.80 (0.04)	18.59	< .001	[0.71, 0.88]
Anmerkung. N = 100. KI = Konfidenzintervall für b; ^aPrädiktoren zentriert; ^bZusätzlich erklärter Varianzanteil durch Interaktionsterm: F(1, 96) = 75.16, p < .001; ^cF(2, 96) = 193.43, p < .001.

#08 Literatur

Schneider, K., Schwark, M. Die goldene Mitte finden: Auswirkung der Homeoffice-Intensität auf Arbeitsleistung und Arbeitszufriedenheit im Kontext der Ressourcenerhaltung. Gr Interakt Org 54, 421–436 (2023). https://doi.org/10.1007/s11612-023-00696-3